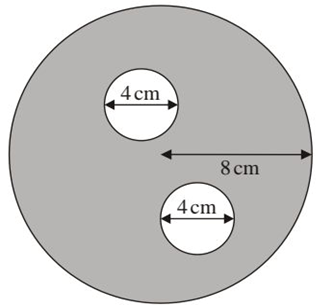
The diagram below shows two small circles inside a large circle. The large circle has a radius of 8 cm while each of the small circles has a diameter of 4 cm.Calculate area of the shaded region.
A: 150.79
B: 188.49
C: 176
D: 201.06
To find the area of the shaded region, we have to add the area of the two inner circles and less their area from the area of the bigger circle.
using the formulae A = πr²
Area of the Bigger circle
A = πr²
A = (22/7) × 8²
= 201.14 cm²
Area of one small circle
A = πr²
A = (22/7)×2² (since the diameter is 4, we divide by two to get the radius)
= 12.57 cm²
since the circles are the same in radius, we multiply by 2 to get the area of the two inner circles altogether
Total area = 12.57 cm² * 2 = 25.14 cm²
Area of shaded region, we will subtract our findings of the small circles from the area of the bigger circle.
Area of shaded = 201.14 cm² - 25.14 cm²
A = 176cm²
With a focus on mathematical calculations, Learnerscamp provides dynamic tutorials, real-world applications, and problem-solving scenarios that empower students to grasp mathematical concepts with ease. Our adaptive learning algorithms ensure personalized learning paths, allowing students to progress at their own pace while receiving instant feedback to reinforce their understanding.
Learnerscamp goes the extra mile by incorporating a robust assessment system that enables students to gauge their understanding through comprehensive tests. Our adaptive testing module dynamically tailors assessments to each student's proficiency level, providing a personalized evaluation of their mathematical knowledge.
sample Question screanshot

Upon completing a test, students receive a detailed and insightful report that not only highlights their overall performance but also breaks down their scores on a per-question basis. This granular analysis allows students to identify specific areas that may need improvement fostering a targeted and efficient approach to learning.
sample report screanshot