In mathematics, integers form the foundation for understanding numerical operations and solving a wide range of problems. From addition and subtraction to multiplication and division, mastering integer calculations is essential for navigating the complexities of mathematical concepts and real-life scenarios. Hence, this blog in exploring the multiplication and division of Integers, focusing on obtaining products of positive and negative integers, working with both negative integers in multiplication and division, and providing practical illustrations to guide your learning journey. Therefore, by the end of this exploration, you’ll be equipped with the knowledge and skills to confidently perform integer calculations and tackle real-world challenges involving multiplication and division of integers.
Before we delve deeper into exploring the multiplication and division of integers, I would like to remind you as a learner that LearnersCamp provides additional insights into these disparities. Additionally, LearnersCamp has grown to become a valuable platform for learners seeking to deepen their understanding of mathematical concepts, including integers and use of numberline. Moreover, it has a user-friendly interface and a vast array of educational materials, including articles, tutorials, and interactive quizzes; LearnersCamp offers comprehensive guidance on such topics. Hence, by visiting LearnersCamp, learners can access clear explanations, practical examples, and engaging exercises to solidify their grasp of these fundamental mathematical principles.
Understanding Integer Multiplication:
Multiplication of integers involves combining numbers to obtain a product. As such, let us explore the different scenarios of integer multiplication:
- Products of Positive and Negative Integers:
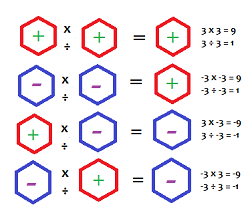
When multiplying positive and negative integers, the product is negative. Let’s illustrate this concept: Example 1:
Multiply 6 by -4. Solution:
6 x (-4) = -24 In this example, multiplying a positive integer (6) by a negative integer (-4) results in a negative product (-24). - Products of Two Negative Integers:
Multiplying two negative integers yields a positive product. Let’s see an example: Example 2:
Multiply -3 by -5. Solution:
(-3) x (-5) = 15 Here, the product of two negative integers (-3 and -5) is positive (+15).
- Practical Illustration:
Consider a scenario where a company’s revenue and expenses are represented by positive and negative integers, respectively. The product of these integers represents the net profit or loss.
Example:
Revenue: +$500
Expenses: -$300
Solution:
Revenue x Expenses = 500 x (-300) = -$150,000
In this example, the negative product indicates a net loss of $150,000.
Understanding Integer Division:
Division of integers involves distributing a quantity into equal parts or determining the number of times one quantity is contained within another. Let’s explore different scenarios of integer division:
- Division of Integers Where One Integer is Negative:
When dividing a positive integer by a negative integer or vice versa, the quotient is negative. Let’s see an example: Example 3:
Divide 15 by -3. Solution:
15 ÷ (-3) = -5 Here, dividing a positive integer (15) by a negative integer (-3) results in a negative quotient (-5). - Division of Integers Where Both Integers are Negative:
Dividing two negative integers yields a positive quotient. Let’s illustrate this concept: Example 4:
Divide -20 by -4. Solution:
(-20) ÷ (-4) = 5 In this example, dividing two negative integers (-20 and -4) results in a positive quotient (5).
- Practical Illustration:
Consider a scenario where a team’s total distance traveled and the number of hours taken to complete the journey are represented by positive integers. The quotient of these integers represents the average speed.
Example:
Total Distance: 300 miles
Time Taken: 6 hours
Solution:
Total Distance ÷ Time Taken = 300 ÷ 6 = 50 miles per hour
In this example, the positive quotient indicates an average speed of 50 miles per hour.
Conclusion:
In conclusion, exploring the multiplication and division of Integers is essential for solving mathematical problems and analyzing real-life situations involving quantities and quantities. Thus, by mastering the principles of integer multiplication and division, you’ll be equipped to perform accurate calculations and make informed decisions in various contexts. Moreover, through practical illustrations and examples, we’ve explored the intricacies of integer multiplication and division, reinforcing key concepts and techniques. So, whether you’re managing finances, analyzing data, or solving mathematical problems, remember to apply the principles of integer multiplication and division to achieve accurate and meaningful results.